Draw Curves with Straight Lines
In this activity you will use straight lines to draw beautiful curved shapes with a simple mathematical mapping process.
Suitable for KS2-4.  Curriculum links Mathematics: Geometry, Multiplication, Patterns and Sequences 
instructions_epicycloid.pdf
File Size: 1055 kb
File Type: pdf
Download File
template_epicycloid_100.pdf
File Size: 707 kb
File Type: pdf
Download File
template_epicycloid_50.pdf
File Size: 650 kb
File Type: pdf
Download File
​Mapping is used many fields of mathematics, including the design of metamaterials (special materials with properties not found in nature).  At its simplest, mapping is a way of assigning each object in a set to an object in another set using some kind of transformation.  The objects can be drawn with connecting lines or arrows.  Find out more about mapping here.

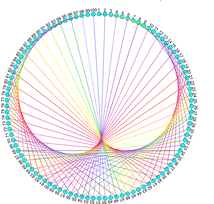
In this activity you can draw curved shapes called epicycloids by using multiplication to connect points around a circle.
What is an Epicycloid?
​If we roll a circle around the circumference of another circle, the shape traced by a point on the moving circle is an epicycloid.
The type of epicycloid depends on the relative sizes of the circles.
If the circles are the same size, we get a squashed heart shape called a cardioid (the name comes from the Greek kardia, meaning heart)
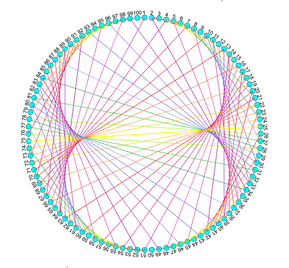
If the rolling circle is half the diameter of the fixed one, we get a nephroid (from the Greek nephros, meaning kidney).  ​
​Here is the shape we get if the diameter of the rolling circle is one third the diameter of the fixed.
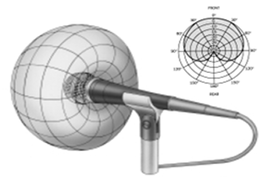
These shapes occur in nature: many leaves have a heart-like cardioid shape.  Next time you have a cup of tea, you might notice a cardioid or nephroid appear in the light reflecting on the surface!  ​In sound engineering, cardioid microphones pick up sound in a cardioid shape, taking more sound from the front and sides than from behind.
Picture
Photograph by Dominicus Johannes Bergsma, distributed under a CC BY-SA 4.0 license. creativecommons.org/licenses/by-sa/4.0/deed.en
Picture
Image by Tóth Péter distributed under a CC BY-SA 3.0 license. creativecommons.org/licenses/by-sa/3.0/deed.en
Draw an Epicycloid
You will need a ruler, coloured pens or pencils, and the instructions and 100-dots or 50-dots template you can download here:
instructions_epicycloid.pdf
File Size: 1055 kb
File Type: pdf
Download File
template_epicycloid_100.pdf
File Size: 707 kb
File Type: pdf
Download File
template_epicycloid_50.pdf
File Size: 650 kb
File Type: pdf
Download File
  1. For a cardioid, join each point on the circle to the point 2 x its number value with a straight line (join 1 to 2, 2 to 4, 3 to 6 and so on).  You can fill in the table to help you.
  2. There are 100 points on the circle.  When you get to point 51, which maps to 102, keep going round the circle, subtracting 100 from the number you need, to find the correct point. 
  3. Point 2 is now point 102, point 22 is now point 122.  This is called modular arithmetic.  We use it every day when we convert between the 12 and 24 hour clocks!
  4. Don't worry if you make a mistake.  Small mistakes won't show up much.
  5. Keep going until you have joined 99 to 198.  Your cardioid is finished!

​If you want a shorter activity try the 50-dots template.  When you get to point 26, which maps to 52, subtract 50 from the number you need (mapping 26 onto 2,  27 onto 4, and so on).
String Art Epicycloid
To make a string art epicycloid  you will need cardboard, scissors, glue and thread, yarn or string. 

​Download the instructions and give it a try!
Other Epicycloids

Try using different multiples for the mapping.  Multiplying by 3 gives a nephroid.  What happens with higher multiples?
Learn More