This lesson and the accompanying worksheets will help you identify types of waves and their key properties.
What is a wave?
A mechanical wave is a disturbance that travels through something. We call the something through which the wave travels a medium. The medium could be air, water or any substance.
Electromagnetic waves such as light can travel through a vacuum. Their vibrations are changes in their electrical and magnetic fields.
Electromagnetic waves such as light can travel through a vacuum. Their vibrations are changes in their electrical and magnetic fields.
A key definition to remember about waves is that they transport energy without transporting matter.
When a phone rings the air around the phone vibrates. The vibrations travel as the vibrating air particles cause the ones next to them to vibrate, and so on until they reach our ears. We call this a sound wave. But the air particles do not travel between the phone and our ear, it is the vibrational disturbance that travels:
Wavemachine animation by Lookang and Wolfgang Christian is the original author of the computer model using Easy Java Simulations (EJS) version 4.3 authoring and modelling tool created by Francisco Esquembre. CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=20983499
Types of Wave
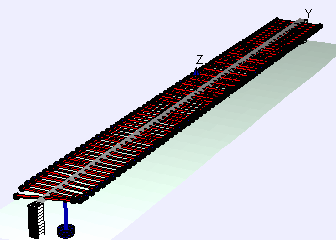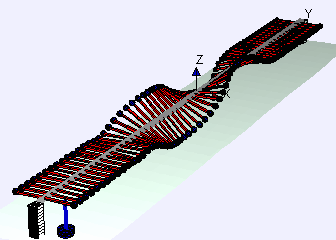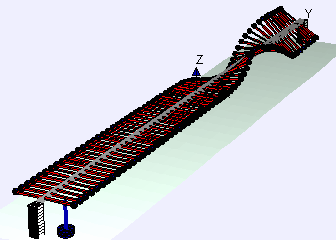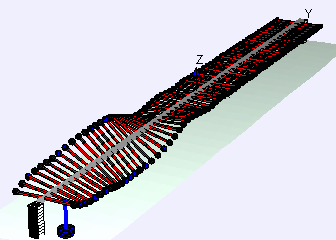
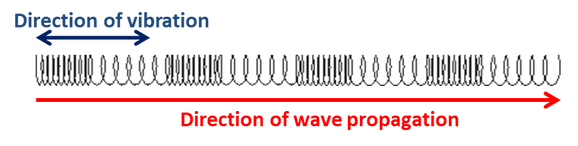
Waves can be defined by the direction of oscillation (vibration) compared to the direction the wave propagates (travels). We can describe two types of wave, longitudinal and transverse, using a slinky:
Transverse waves vibrate perpendicular (at right angles) to the direction of travel
Try it: Hold each end of a slinky in one hand, with your hands about a metre apart. Move one end of the slinky up and down with small hand movements, holding the other end still.
A transverse wave on a slinky
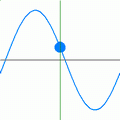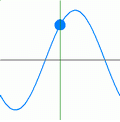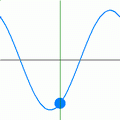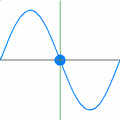
A transverse wave has moving peaks (or crests) and troughs (valleys) which are the highest and lowest points in the medium. They are the furthest positions from the centre equilibrium position.
Ripples in water are transverse waves.
Ripples in water are transverse waves.
Longitudinal waves vibrate parallel to the direction of travel
Try it: Hold each end of a slinky in one hand, with your hands about a metre apart. Move one end of the slinky back and forth (towards and away from your other hand) with small hand movements, holding the other end still.
A longitudinal wave on a slinky
A longitudinal wave has compressions and rarefactions (or expansions) where the particles (or coils in the slinky) are closest together and furthest apart.
Sound waves are longitudinal.
Sound waves are longitudinal.
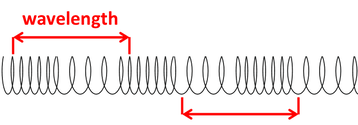
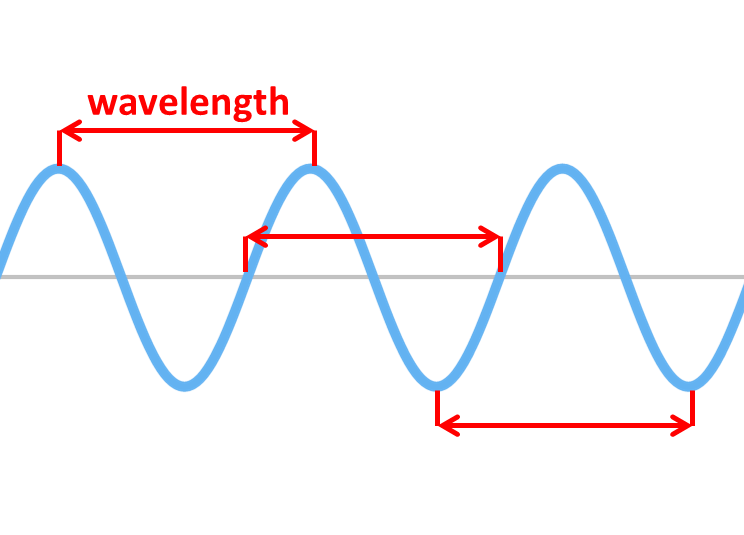
Wavelength
WAVELENGTH is the length of a complete wave, measured between a point on one wave and the same point on the next.
|
|
Wavelengths can range from the very tiny to the very big.
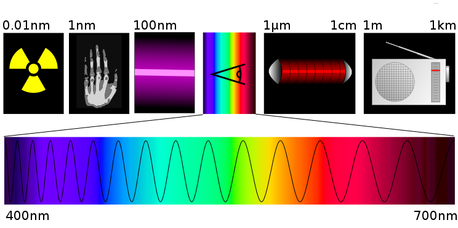
Light visible to humans has wavelengths between about 400 and 700 nanometres (a nanometre is one billionth of a metre). Different colours have different wavelengths. The image below compares the wavelengths of gamma rays (the shortest), X-rays, ultraviolet, visible, infrared and radio waves (the longest shown), and shows the visible colour spectrum from violet to red.
Light visible to humans has wavelengths between about 400 and 700 nanometres (a nanometre is one billionth of a metre). Different colours have different wavelengths. The image below compares the wavelengths of gamma rays (the shortest), X-rays, ultraviolet, visible, infrared and radio waves (the longest shown), and shows the visible colour spectrum from violet to red.
Image credit: Tatoute and Phrood / CC BY-SA (http://creativecommons.org/licenses/by-sa/3.0/)
Sound waves audible to humans have wavelengths between about 1.7 millimetres (for the highest pitched sounds) and 17 metres (for the lowest pitched).
Wavelength is represented by the Greek letter lambda, λ.
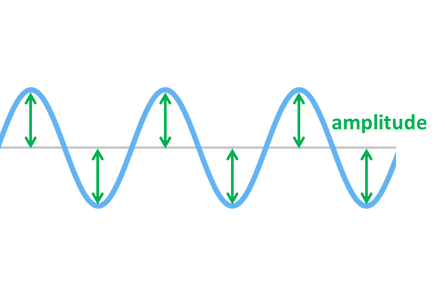
Amplitude
The amplitude of a wave is its maximum disturbance from its equilibrium (undisturbed) position
It is important to remember that amplitude is not the difference between the highest and lowest points of the wave.
Amplitude in a transverse wave is measured from the top of a crest to the centre, or from the bottom of the trough to the centre:
Amplitude in a transverse wave is measured from the top of a crest to the centre, or from the bottom of the trough to the centre:
Amplitude in a transverse wave
Amplitude in longitudinal waves is a measure of how close together the particles are in a compression, or how far apart they are in a rarefaction compared to the undisturbed particles.
High amplitude longitudinal waves have very squashed-together compressions and very spread-out rarefactions. We can represent this with the coils on our slinky:
High amplitude longitudinal waves have very squashed-together compressions and very spread-out rarefactions. We can represent this with the coils on our slinky:
Higher and lower amplitude longitudinal waves on a slinky
The greater the amplitude of a light wave the brighter the light.
The greater the amplitude of a sound wave the louder the sound.
The greater the amplitude of a sound wave the louder the sound.
Frequency
The frequency, f of a wave is the number of waves that pass a fixed point in one second
In the animation below the frequency can be found by counting the number of times the blue marker reaches the top in one second.
Wave animation.
Credit: user:ikaxer derivative work: Dave3457 distributed under a CC BY-SA license (https://creativecommons.org/licenses/by-sa/3.0)
Frequency is measured in hertz (Hz) or kilohertz (kHz). One Hz is equal to one cycle (one wave) per second. One kHz = one thousand Hz.
High frequency sounds are high pitched, and low frequency sounds are low pitched. Humans can hear sound frequencies between about 20 Hz and 20 kHz. Sounds with frequencies higher than this range are called ultrasound. Ultrasound is used in medical imaging. Sounds with frequencies lower than humans can hear are called infrasound. Elephants use infrasound to communicate over long distances.
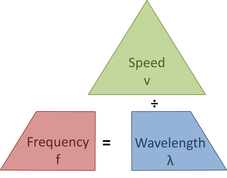
The time period, T of a wave is the time taken for one wave to pass a fixed point. The time period can be found using the formula T = 1/f
High frequency sounds are high pitched, and low frequency sounds are low pitched. Humans can hear sound frequencies between about 20 Hz and 20 kHz. Sounds with frequencies higher than this range are called ultrasound. Ultrasound is used in medical imaging. Sounds with frequencies lower than humans can hear are called infrasound. Elephants use infrasound to communicate over long distances.
The time period, T of a wave is the time taken for one wave to pass a fixed point. The time period can be found using the formula T = 1/f
Wave Speed
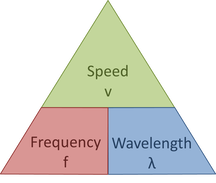
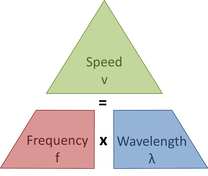
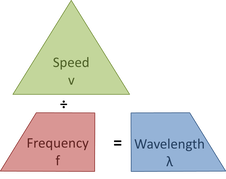
Wave speed (v) in metres per second is equal to the frequency (f) in Hz multiplied by the wavelength ( λ) in m
v = f λ
v = f λ
The wave speed equation is represented by the formula triangle below:
|
|
|
Sound waves travel at a speed of about 340 m/s in air, and close to 1500 m/s in water.
Light waves travel at a speed of nearly 300,000,000 m/s in a vacuum.
Light waves travel at a speed of nearly 300,000,000 m/s in a vacuum.
Download Worksheets
|
Printable worksheet with revision questions.
|
Printable vocabulary revision sheet
|
|
| ||||||||