The Science of Balloons Part 1: Under Pressure |
KS4 & 5 / CfE Senior:
Material Properties |
|
Experiments with balloons can help us learn about material behaviour, elasticity and viscoelasticity.
In Part 1 we examine the famous Two Balloon experiment and find out why inflating a balloon is not always easy. |
QUESTION: A large and a small balloon are connected by a tube with taps.
Can you predict what happens when the taps are opened so that air can move between the balloons?
Can you predict what happens when the taps are opened so that air can move between the balloons?
This problem was posed by American physicist and television personality Julius Sumner Miller in the American Journal of Physics in 1952 [1], and has been widely discussed ever since.
CLUE: Think about blowing up a balloon. At what stage is it hardest to inflate: at the start, the middle or the end?
When you have made your prediction, watch the video below to see if you were correct.
THE SOLUTION: Most people predict that both balloons will end up the same size, but in fact the small balloon gets smaller and the big balloon gets bigger. Air moves from the smaller to the bigger balloon!
Why does this happen?
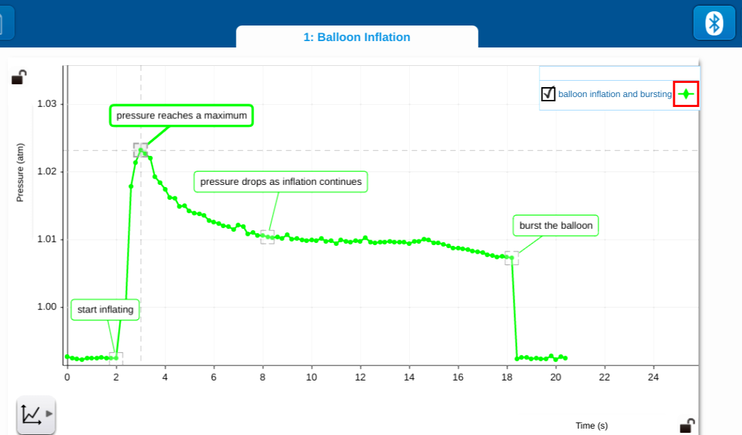
Using a wireless pressure sensor, we can measure the pressure inside a balloon as we inflate it. Our graph represents pressure vs time, but a graph of pressure vs balloon radius would have a very similar shape. The balloon gets bigger as we inflate it, so we can consider the inflation time as a rough approximation for its radius.
Using a wireless pressure sensor, we can measure the pressure inside a balloon as we inflate it. Our graph represents pressure vs time, but a graph of pressure vs balloon radius would have a very similar shape. The balloon gets bigger as we inflate it, so we can consider the inflation time as a rough approximation for its radius.
The pressure increases very quickly at first, and reaches a maximum when the balloon is still small (when the balloon has expanded by approximately 40% of its initial radius [3]). Then the pressure drops as we continue to inflate the balloon. So the pressure inside the small balloon is greater than the pressure inside the large balloon. We experience this when we blow up a balloon: the first stage is the hardest, and once the balloon has inflated a little, the task becomes much easier.
When the taps are opened, the pressure equalises. Air moves from the small to the large balloon, making the large balloon larger and the small balloon smaller. This continues until their sizes lie on either side of the pressure maximum, at a point where the pressures are equal.
When the taps are opened, the pressure equalises. Air moves from the small to the large balloon, making the large balloon larger and the small balloon smaller. This continues until their sizes lie on either side of the pressure maximum, at a point where the pressures are equal.
Why is the pressure higher in the smaller balloon?
There are two factors that contribute to this. We must consider the curved shape of the balloon, and the material it is made from.
There are two factors that contribute to this. We must consider the curved shape of the balloon, and the material it is made from.
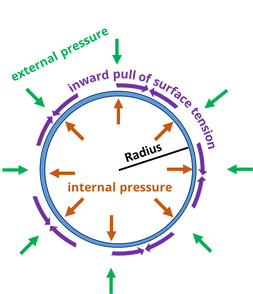
A balance of forces: The pressure inside an inflated balloon is greater than the pressure outside it. The balloon is stable because the expanding force due to the pressure difference is balanced by the contracting force exerted by the surface tension of the rubber.
Laplace's Law for the pressure in spherical bubbles and droplets tells us that:
ΔP = 2γ /r for a droplet with one surface
and
ΔP = 4γ /r for a bubble with an inside and an outside surface
ΔP is the pressure difference between the interior and exterior of the droplet or bubble, γ is the surface tension, and r is the radius.
It shows us that where the surface tension is equal and wall thickness negligible, the pressure inside a bubble is inversely proportional to its radius of curvature. The smaller the bubble, the higher its internal pressure.
To apply this to the balloons, we are making several approximations. For example, we know that the surface tension of the two balloons is not uniform, and they are not perfect spheres. Mathematicians and physicists have modelled the problem in detail to arrive at a closer approximation of the a real balloon [2-4].
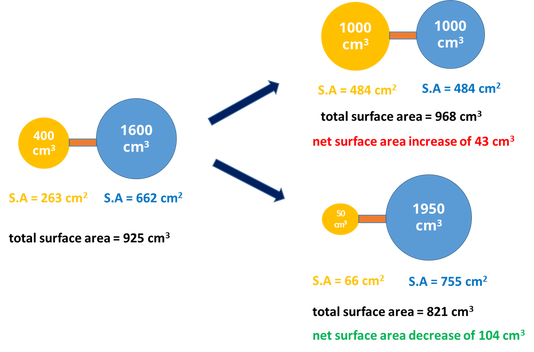
Surface Area: Another way to consider the problem is to examine the change in the amount of stretch in the balloons. To stretch a balloon and increase its surface area requires energy. Imagine two spherical balloons share a total volume of 2 litres of air. At first the air is distributed between the balloons unequally. When we open the tap between them, the total volume remains constant, but it can now be shared between the two balloons in different ways.
ΔP = 2γ /r for a droplet with one surface
and
ΔP = 4γ /r for a bubble with an inside and an outside surface
ΔP is the pressure difference between the interior and exterior of the droplet or bubble, γ is the surface tension, and r is the radius.
It shows us that where the surface tension is equal and wall thickness negligible, the pressure inside a bubble is inversely proportional to its radius of curvature. The smaller the bubble, the higher its internal pressure.
To apply this to the balloons, we are making several approximations. For example, we know that the surface tension of the two balloons is not uniform, and they are not perfect spheres. Mathematicians and physicists have modelled the problem in detail to arrive at a closer approximation of the a real balloon [2-4].
Surface Area: Another way to consider the problem is to examine the change in the amount of stretch in the balloons. To stretch a balloon and increase its surface area requires energy. Imagine two spherical balloons share a total volume of 2 litres of air. At first the air is distributed between the balloons unequally. When we open the tap between them, the total volume remains constant, but it can now be shared between the two balloons in different ways.
The total surface area depends on how the volume of air is shared:
If the balloons equalise in volume, there is a net gain in surface area, and therefore an increase in the total amount of stretch. This requires energy to be added to the system.
If the difference between the volumes is increased, however, there is a net loss in surface area. The decrease in surface area of the small balloon is greater than the increase in surface area of the large balloon. This reduces the total stretch in the system.
If the balloons equalise in volume, there is a net gain in surface area, and therefore an increase in the total amount of stretch. This requires energy to be added to the system.
If the difference between the volumes is increased, however, there is a net loss in surface area. The decrease in surface area of the small balloon is greater than the increase in surface area of the large balloon. This reduces the total stretch in the system.
What are balloons made of?
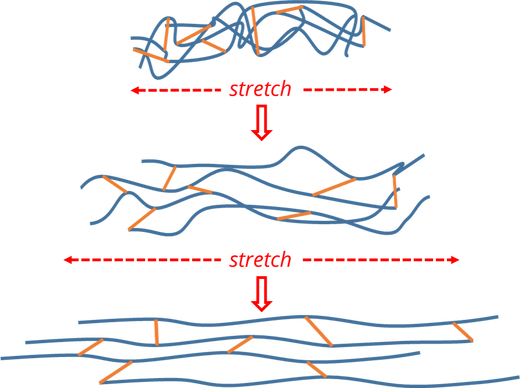
Balloons are made from rubber latex, a polymer consisting of long chains which are linked together (cross-linked) in multiple places along their length. This structure accounts for the material's elastic behaviour.
When the material not under strain, the polymer chains are coiled and tangled around each other randomly. When we stretch the rubber, the chains straighten and line up. This reduces the number degrees of freedom (the number of ways we can arrange the chains and links), and makes the system more ordered (lower entropy).
When the material not under strain, the polymer chains are coiled and tangled around each other randomly. When we stretch the rubber, the chains straighten and line up. This reduces the number degrees of freedom (the number of ways we can arrange the chains and links), and makes the system more ordered (lower entropy).
Entropy is often called disorder. The more degrees of freedom in a system the higher its entropy. The second law of thermodynamics tells us that the entropy in an isolated system will increase, and spontaneous change is associated with an increase in entropy. To stretch the rubber we need to input energy, and when we release it, it will spontaneously return to its coiled up, more disordered state.
The change in entropy varies as we stretch the rubber. At first, there is a large reduction in entropy as the molecules begin to untangle, so the initial stretching requires more force. Then with further stretching the change in entropy is less, and stretching gets easier. If we keep on stretching, the polymer chains eventually become fully extended, and we begin to pull on the cross-links, so stretching gets more difficult again.
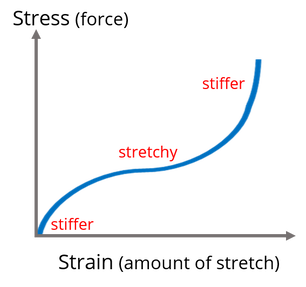
This means that the elasticity of rubber changes as it is stretched. The graph of the stress (applied force per unit area) vs strain (the degree of stretch) for rubber is not linear. It has an initial steep region, where the rubber is stiffer, a middle region where the material is easier to stretch, and then another steep region.
The change in entropy varies as we stretch the rubber. At first, there is a large reduction in entropy as the molecules begin to untangle, so the initial stretching requires more force. Then with further stretching the change in entropy is less, and stretching gets easier. If we keep on stretching, the polymer chains eventually become fully extended, and we begin to pull on the cross-links, so stretching gets more difficult again.
This means that the elasticity of rubber changes as it is stretched. The graph of the stress (applied force per unit area) vs strain (the degree of stretch) for rubber is not linear. It has an initial steep region, where the rubber is stiffer, a middle region where the material is easier to stretch, and then another steep region.
That is why the first stage of blowing up a balloon is the hardest, and why in the two balloon experiment, it is easier to increase the size of the large balloon than the small.
But this is not the whole story. Why do we stretch a balloon before we inflate it? Why does a rubber band heat up when it is repeatedly stretched and released? What is viscoelasticity and why do we research it?
[1] Miller, J. S. (1952) "Pressure within a bubble" Am. J. Phys., 20, 115.
[2] Merritt, D. & Weinhaus, F. (1978) "The pressure curve for a rubber balloon" Am. J. Phys., 46, 976-977
[3] Stein, R. F. (1958) "On the inflating of balloons" J. Chem. Educ., 35(4): 203-204
[4] Weinhaus, F. and Barker, W. (1978) "On the equilibrium states of interconnected bubbles or balloons"
Am. J. Phys. 46, 978-982
[2] Merritt, D. & Weinhaus, F. (1978) "The pressure curve for a rubber balloon" Am. J. Phys., 46, 976-977
[3] Stein, R. F. (1958) "On the inflating of balloons" J. Chem. Educ., 35(4): 203-204
[4] Weinhaus, F. and Barker, W. (1978) "On the equilibrium states of interconnected bubbles or balloons"
Am. J. Phys. 46, 978-982