Find out about the phenomenon of resonance and try out some experiments that explore it.
If we pass sound waves through a metal plate covered in sand, at certain frequencies an extraordinary thing happens: The sand appears to form patterns spontaneously.
The frequencies at which these patterns occur are called resonant frequencies. In this post we will explore resonance.
Before we start: If you need a reminder of wave vocabulary take a look at the anatomy of a wave.
Before we start: If you need a reminder of wave vocabulary take a look at the anatomy of a wave.
Wave InterFerence
When two waves with the same wavelength and frequency add together, the resulting wave depends on how the peaks and troughs line up.
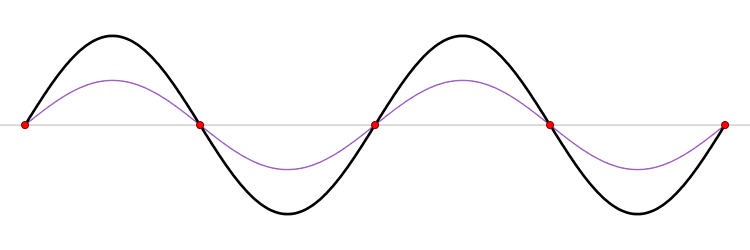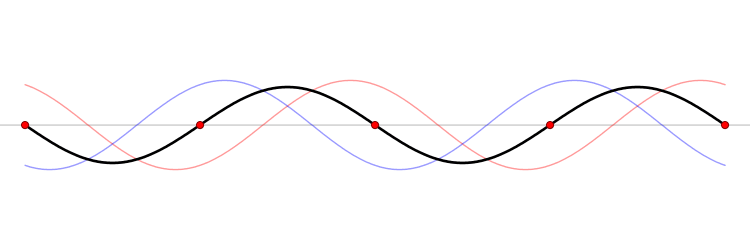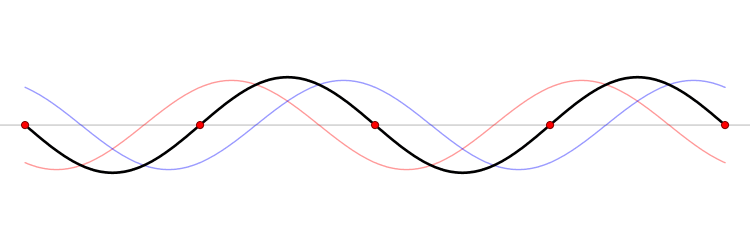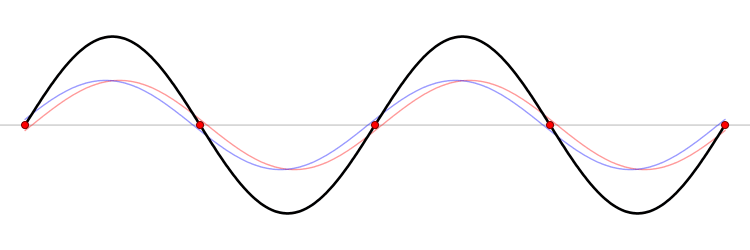
If the peaks of the first wave line up with the peaks of the second, the result is a wave with an amplitude equal to the sum of the amplitudes of the individual waves. We call this constructive interference.
If the peaks of the first line up with the troughs of the second, the resulting wave has an amplitude equal to the difference between their amplitudes. This is called destructive interference. If both waves have the same amplitude they cancel completely. Destructive interference is used in noise cancellation.
If the peaks of the first line up with the troughs of the second, the resulting wave has an amplitude equal to the difference between their amplitudes. This is called destructive interference. If both waves have the same amplitude they cancel completely. Destructive interference is used in noise cancellation.
Standing Waves
Now imagine a wave being reflected from a surface. The way the original wave and the reflected wave combine will depend on timing:
At certain frequencies, the interference of the two waves results in a wave that appears to oscillate in place, but not travel. We call it a standing, or stationary wave. Look at the animation below and notice the fixed points where the red and blue waves always cancel: the resulting standing wave oscillates about these points, called nodes.
At certain frequencies, the interference of the two waves results in a wave that appears to oscillate in place, but not travel. We call it a standing, or stationary wave. Look at the animation below and notice the fixed points where the red and blue waves always cancel: the resulting standing wave oscillates about these points, called nodes.
Animation of the formation of a standing wave. Public domain image. Credit: Lucas Vieira
Try it
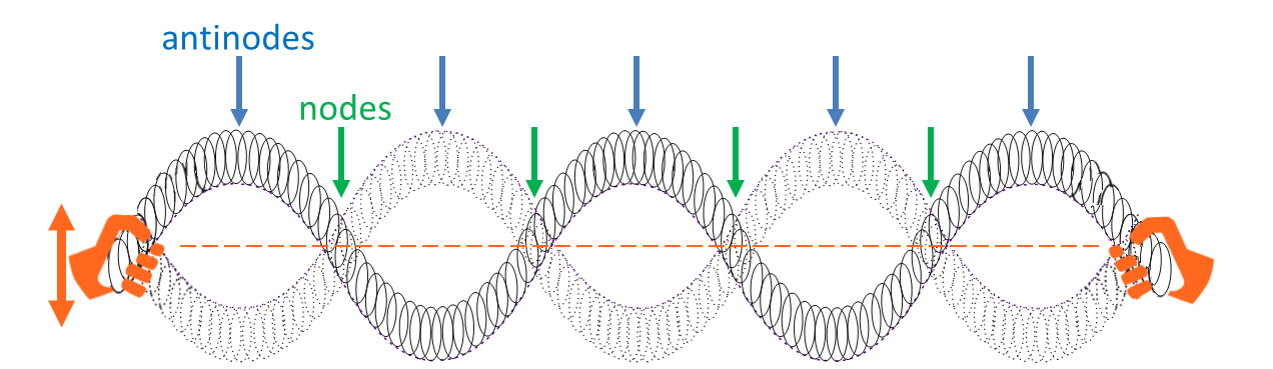
Hold each end of a slinky in one hand, with your hands about a metre apart. Move one end of the slinky up and down with small hand movements, holding the other end still. With a bit of practice you should be able to make a standing wave on the slinky.
Hold each end of a slinky in one hand, with your hands about a metre apart. Move one end of the slinky up and down with small hand movements, holding the other end still. With a bit of practice you should be able to make a standing wave on the slinky.
You will notice points on the wave where the slinky is not oscillating. These points are the nodes. The points where oscillations are largest (have the biggest amplitude) are called antinodes. Antinodes and nodes alternate along the standing wave.
You might notice that if you get the timing right, it only takes a small movement of your hand to produce a large amplitude standing wave on the slinky. This is because standing waves are associated with resonance.
You might notice that if you get the timing right, it only takes a small movement of your hand to produce a large amplitude standing wave on the slinky. This is because standing waves are associated with resonance.
resonance
The resonant, or natural frequency of an object is the frequency at which it tends to vibrate. The natural frequency of an object depends on factors including its stiffness. Resonance occurs when an object is subject to a driving force at its natural frequency. The object will vibrate strongly and a small driving force can set up a very large amplitude oscillation, as we saw with the slinky.
Try it
Here is an experiment you can try, that demonstrates resonance:
Cut 3 strips of paper about 2.5 cm wide, and of different lengths ranging between about 20 cm and 50 cm. Join the ends of each strip so that it forms a ring and tape all three rings in a row down the centre of a length of cardboard
Here is an experiment you can try, that demonstrates resonance:
Cut 3 strips of paper about 2.5 cm wide, and of different lengths ranging between about 20 cm and 50 cm. Join the ends of each strip so that it forms a ring and tape all three rings in a row down the centre of a length of cardboard
Starting slowly, shake the cardboard from side to side. Gradually increase the speed. All the rings will move, but at certain rates of shaking, one ring will move in large oscillations as the shaking matches its natural resonant frequency. Try to make each ring in turn resonate. The smallest, stiffest ring will have the highest resonant frequency and the largest ring the slowest.
Sympathetic Vibration
If two objects have the same resonant frequency, the vibrations of one can trigger vibrations in the other. We call this sympathetic vibration, or sympathetic resonance. Watch this clip of sympathetic vibrations in wine glasses:
The slip and stick movement the finger on the rim of the glass makes it vibrate and causes the sound. Both glasses have the same natural frequency, so when the sound waves from the singing glass reach the other glass, it starts to resonate, and the vibrations cause the candle to fall.
Try it
Here is an experiment you can do at home that explores sympathetic vibrations in pendulums:
Here is an experiment you can do at home that explores sympathetic vibrations in pendulums:
These home-made pendulums are made from washers on strings. They are tied to a straw that is threaded onto a string suspended from a support. We used a washing airer to support ours. There are five pendulums, of two different lengths.
The time taken for a simple pendulum to swing back and forth is proportional to the square root of its length. If it starts at a very small angle, its time period can be approximated using the formula:
T = 2π√(L/g)
where
T is the time period in seconds (s)
L is the length of the pendulum in metres
g is the acceleration due to gravity (9.8 m/s²)
The frequency, f (the number of back and forth swings per second), is the inverse of the time period:
f = 1/T
So pendulums with the same length have the same time period and natural frequency. Short pendulums have a shorter time period and oscillate at a higher frequency than long pendulums.
When we set one pendulum in motion, its movements pull on the straw and on the other pendulums. All the pendulums move a little, but the one which is same length as the first has the same resonant frequency, and it begins to oscillate with a large amplitude.
The pendulums are swinging out of phase, and each movement of the second pendulum pulls back a little on the first. The amplitude of the first is reduced until almost all its energy has been transferred to the second, which now swings with a large amplitude. The reverse process now happens, and energy is transferred back to the first pendulum. Energy is transferred back and forth between the two until all the energy has been lost to friction and air resistance.
Can you explain what happens to the energy when three pendulums have the same length?
The time taken for a simple pendulum to swing back and forth is proportional to the square root of its length. If it starts at a very small angle, its time period can be approximated using the formula:
T = 2π√(L/g)
where
T is the time period in seconds (s)
L is the length of the pendulum in metres
g is the acceleration due to gravity (9.8 m/s²)
The frequency, f (the number of back and forth swings per second), is the inverse of the time period:
f = 1/T
So pendulums with the same length have the same time period and natural frequency. Short pendulums have a shorter time period and oscillate at a higher frequency than long pendulums.
When we set one pendulum in motion, its movements pull on the straw and on the other pendulums. All the pendulums move a little, but the one which is same length as the first has the same resonant frequency, and it begins to oscillate with a large amplitude.
The pendulums are swinging out of phase, and each movement of the second pendulum pulls back a little on the first. The amplitude of the first is reduced until almost all its energy has been transferred to the second, which now swings with a large amplitude. The reverse process now happens, and energy is transferred back to the first pendulum. Energy is transferred back and forth between the two until all the energy has been lost to friction and air resistance.
Can you explain what happens to the energy when three pendulums have the same length?
Visualising resonance: the Chladni plate
The pendulums oscillate at a single frequency, but most vibrating objects have several resonant frequencies. The lowest resonant frequency is called the fundamental frequency.
When sounds at the resonant frequencies are passed through the Chladni plate, waves propagate from the centre of the plate and are reflected at the edges.
Two-dimensional standing wave patterns form, with nodes and antinodes. The sand is shaken off the antinodes, where the vibrations are strongest, and settles in the nodes where the vibrations cancel and the plate is still.
At higher resonant frequencies, the standing waves become more complex, and intricate patterns appear in the sand.
When sounds at the resonant frequencies are passed through the Chladni plate, waves propagate from the centre of the plate and are reflected at the edges.
Two-dimensional standing wave patterns form, with nodes and antinodes. The sand is shaken off the antinodes, where the vibrations are strongest, and settles in the nodes where the vibrations cancel and the plate is still.
At higher resonant frequencies, the standing waves become more complex, and intricate patterns appear in the sand.
Why is resonance important?
Resonance affects our everyday lives in many ways. Here are some examples.
|
Music
When we listen to music we are hearing resonance in action. Musical instruments rely on resonance for sound amplification and to produce notes of a specific pitch, or frequency. In wind instruments, the sound is produced by a standing wave in a vibrating column of air in a pipe. The resonant frequency is controlled by the length of the pipe. The pitch of a note depends on its frequency, so the musician produces different notes by altering the length of the pipe using valves, or by covering and uncovering holes. 
A B Flat Trumpet. Image by PJ, distributed under the CC BY-SA 3.0 licence (https://creativecommons.org/licenses/by-sa/3.0/deed.en)
In a stringed instrument, the musician alters the length of a string by pressing on it. The fundamental vibrational frequency of the string depends on its length: a shorter string produces a higher pitched note, and a longer string a lower note. |
Engineering
The famous experiment where a wineglass can be made to shatter using sound is a good example of why resonance must be considered when structures are built. 
Breaking glass with sound using resonance. Image credit: Acs272, distributed under the CC BY-SA 4.0 license (https://creativecommons.org/licenses/by-sa/4.0)
A loud enough sound at the resonant frequency of the glass can set up vibrations that are so large that the structure of the glass eventually fails.
In engineering, the catastrophic failure of a structure due to natural frequency vibrations is called a resonance disaster. These can occur when an external force such as wind, earthquake, the movement of people or vibrations from machines sets up an oscillation at the natural frequency of the structure. Bridges, buildings, pipes and components must be carefully designed to avoid this. In skyscrapers and large bridges, dampers are used which reduce the amplitude of vibrations. Dampers can also be found in cars and washing machines |
Our Research
In the Mathematics of Waves and Materials group we use mathematical modelling to understand and predict the properties of materials and waves. One area of research where an understanding of resonance is of particular importance is noise reduction.
Devices called resonators are often used to cancel unwanted noise with destructive interference, but low frequency noises can be difficult to eliminate due to their long wavelengths. The video below describes how we can use mathematics to solve problems such as this, with the design of novel materials with special noise reducing properties.
In the Mathematics of Waves and Materials group we use mathematical modelling to understand and predict the properties of materials and waves. One area of research where an understanding of resonance is of particular importance is noise reduction.
Devices called resonators are often used to cancel unwanted noise with destructive interference, but low frequency noises can be difficult to eliminate due to their long wavelengths. The video below describes how we can use mathematics to solve problems such as this, with the design of novel materials with special noise reducing properties.