|
QUESTION: Why does stretching a balloon make it easier to inflate? |
In Part 1 we looked at the two-balloon experiment, and found out why the first stage of inflating a balloon is the hardest. Before attempting to blow up a balloon, we often see people stretching it by hand a few times. We know from experience that this makes the inflation easier, but why is this the case?
Viscoelasticity: materials with memory
The rubber latex that balloons are made from is an example of a viscoelastic material. Viscoelastic materials combine the properties of viscous fluids and elastic solids when they are deformed. Other viscoelastic materials include other polymers and many biological tissues.
A defining property of viscoelastic materials is that their response to stress (an applied force per unit of area) and strain (the amount of deformation) is affected by the stresses and strains they have undergone before. Viscoelastic materials could be said to have a memory which affects their behaviour.
A defining property of viscoelastic materials is that their response to stress (an applied force per unit of area) and strain (the amount of deformation) is affected by the stresses and strains they have undergone before. Viscoelastic materials could be said to have a memory which affects their behaviour.
|
Four Key Properties of Viscoelastic Materials:
|
Strain Rate Dependence
Strain rate dependence means that the material responds differently depending on how fast it is stretched or compressed. Pull a piece of Blu-Tack or Silly Putty very quickly and it will snap (behaving more like a solid), pull it slowly and it will stretch and flow (behaving more like a fluid).
Strain rate dependence means that the material responds differently depending on how fast it is stretched or compressed. Pull a piece of Blu-Tack or Silly Putty very quickly and it will snap (behaving more like a solid), pull it slowly and it will stretch and flow (behaving more like a fluid).
Viscoelastic Creep
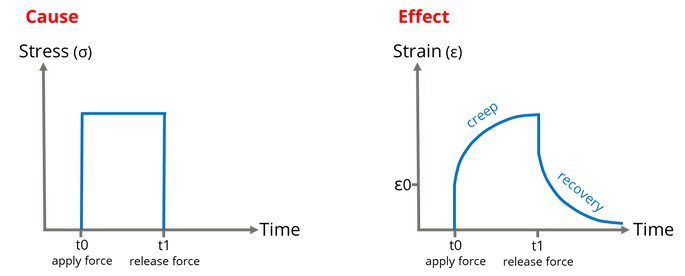
If we apply a force to a viscoelastic material it will deform. If we then maintain the force the material will continue to deform slowly (creep). When the force is removed, the material will not immediately return to its original shape, but will slowly recover over time. Memory foam mattresses are made of viscoelastic material which slowly conforms to the sleeper's body with viscoelastic creep.
The cause and effect graphs below illustrate creep. The stress is the force applied to the material per unit area, and the strain is the deformation in the material in response to the stress. If we apply a stress at time t0, the material will deform with an initial strain (ε0), and then continue to deform until the stress is removed at time t1. When the stress is removed there is an initial immediate drop in strain, followed by a continued slower reduction in strain as the material recovers.
If we apply a force to a viscoelastic material it will deform. If we then maintain the force the material will continue to deform slowly (creep). When the force is removed, the material will not immediately return to its original shape, but will slowly recover over time. Memory foam mattresses are made of viscoelastic material which slowly conforms to the sleeper's body with viscoelastic creep.
The cause and effect graphs below illustrate creep. The stress is the force applied to the material per unit area, and the strain is the deformation in the material in response to the stress. If we apply a stress at time t0, the material will deform with an initial strain (ε0), and then continue to deform until the stress is removed at time t1. When the stress is removed there is an initial immediate drop in strain, followed by a continued slower reduction in strain as the material recovers.
Stress Relaxation
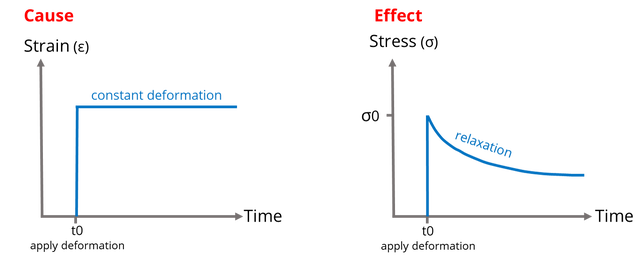
If you put a rubber band around a biscuit tin to hold the lid in place, over time the band holds the lid less securely. This is the result of stress relaxation in the rubber band. Under a constant strain (a deformation such as stretching), the force needed to maintain the deformation in a viscoelastic material gradually reduces.
This is illustrated in the cause and effect graphs below. A constant strain is applied from time t0. There is an immediate stress response which slowly reduces over time as the material relaxes.
If you put a rubber band around a biscuit tin to hold the lid in place, over time the band holds the lid less securely. This is the result of stress relaxation in the rubber band. Under a constant strain (a deformation such as stretching), the force needed to maintain the deformation in a viscoelastic material gradually reduces.
This is illustrated in the cause and effect graphs below. A constant strain is applied from time t0. There is an immediate stress response which slowly reduces over time as the material relaxes.
Hysteresis
In Part 1 we looked at the stress vs strain curve for stretching a rubber balloon, but we did not examine what happens when we release the balloon.
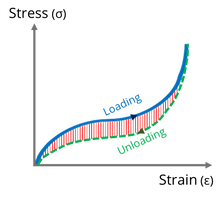
When we stretch a material, energy is stored. When the material is released the stored energy is used to return the material to its original shape.
For a perfectly elastic spring, the energy stored during loading (stretching) is equal to the energy used in unloading. For a viscoelastic material, however, more energy is needed to deform the material than to return it to its original form. The stress-strain curve for unloading does not follow the same path as the loading curve. Instead, the loading-unloading cycle form a loop called a hysteresis loop. The area inside the loop (shaded in red in the diagram below) represents the energy lost as heat during the cycle.
In Part 1 we looked at the stress vs strain curve for stretching a rubber balloon, but we did not examine what happens when we release the balloon.
When we stretch a material, energy is stored. When the material is released the stored energy is used to return the material to its original shape.
For a perfectly elastic spring, the energy stored during loading (stretching) is equal to the energy used in unloading. For a viscoelastic material, however, more energy is needed to deform the material than to return it to its original form. The stress-strain curve for unloading does not follow the same path as the loading curve. Instead, the loading-unloading cycle form a loop called a hysteresis loop. The area inside the loop (shaded in red in the diagram below) represents the energy lost as heat during the cycle.
Stress-strain curve for viscoelastic rubber, showing hysteresis
Try it!
You need two balloons (if you don't have balloons this also works with elastic bands). Quickly stretch and release one of the balloons repeatedly at least 30 times. Then compare the temperature of the balloon you stretched with the one you didn't stretch by holding them gently to your upper lip. The balloon you stretched will feel warmer. Every stretch and release is a loading-unloading cycle with a net release of heat.
Elastic bands and balloons contain latex. Do not do this experiment if you have a latex allergy!
You need two balloons (if you don't have balloons this also works with elastic bands). Quickly stretch and release one of the balloons repeatedly at least 30 times. Then compare the temperature of the balloon you stretched with the one you didn't stretch by holding them gently to your upper lip. The balloon you stretched will feel warmer. Every stretch and release is a loading-unloading cycle with a net release of heat.
Elastic bands and balloons contain latex. Do not do this experiment if you have a latex allergy!
So why does stretching a balloon make it easier to inflate?
If we repeatedly load and unload (stretch and release) a viscoelastic material the amount of energy lost in the hysteresis loop will decrease with each cycle, until an equilibrium is reached.
The force needed to achieve a certain deformation is less with each loading cycle, until we reach equilibrium. This means that when we stretch the material, each subsequent stretch becomes easier. This is known as preconditioning. Repeatedly stretching a balloon preconditions the rubber, making it easier to inflate.
We tested this by putting a pressure sensor inside a balloon and measuring its internal pressure during repeated inflation.
The force needed to achieve a certain deformation is less with each loading cycle, until we reach equilibrium. This means that when we stretch the material, each subsequent stretch becomes easier. This is known as preconditioning. Repeatedly stretching a balloon preconditions the rubber, making it easier to inflate.
We tested this by putting a pressure sensor inside a balloon and measuring its internal pressure during repeated inflation.
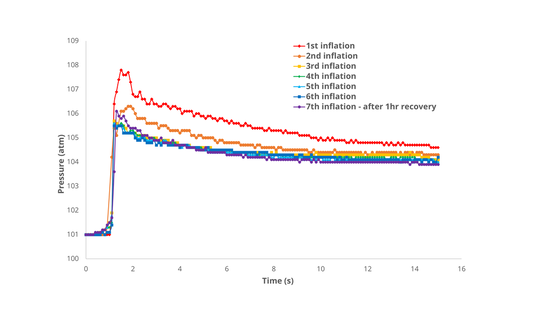
You can see that the second inflation requires less pressure than the first, and the pressure drops again on the third inflation, after which we have reached an equilibrium, and subsequent inflations (4, 5 and 6) follow the same profile as the third.
The 7th inflation was carried out after leaving the balloon to recover for 1 hour. The pressure begins to increase again, but not to its initial value: the material recovery is not complete.
The 7th inflation was carried out after leaving the balloon to recover for 1 hour. The pressure begins to increase again, but not to its initial value: the material recovery is not complete.
Our Research
In our research we use mathematics to model and understand the viscoelastic properties of biological tissues and novel synthetic materials.
Understanding the viscoelastic behaviour of tissues has important medical implications. Recent examples from our group include a study into the inflation of viscoelastic balloons and hollow biological organs such as the bladder [1], and work on the viscoelastic behaviour of tendons [2]. You can find out about our work on tendons in the video below, and in this blog post.
In our research we use mathematics to model and understand the viscoelastic properties of biological tissues and novel synthetic materials.
Understanding the viscoelastic behaviour of tissues has important medical implications. Recent examples from our group include a study into the inflation of viscoelastic balloons and hollow biological organs such as the bladder [1], and work on the viscoelastic behaviour of tendons [2]. You can find out about our work on tendons in the video below, and in this blog post.
Other recent work involved the preparation and cyclic testing of a series of polymer-filled syntactic foams: novel lightweight materials which show excellent damage resistance [3]. You can read about this work here.
Stress-strain curves for unfilled PU and syntactic foams tested up to 70% strain. Inset: Images of the foams after testing. From [3].
[1] De Pascalis, R. Parnell, W.J., Abrahams, I.D., Shearer, T., Daly, D.M., and Grundy, D. (2018) (open access) "The inflation of viscoelastic balloons and hollow viscera" Proc. R. Soc. A 474, 20180102
[2] Shearer, T., Parnell, W. J., Lynch, B., Screen, H. R. C., and David Abrahams, I. (2020) "A Recruitment Model of Tendon Viscoelasticity That Incorporates Fibril Creep and Explains Strain-Dependent Relaxation." J. Biomech. Eng. 142(7), 071003
[3] Yousaf, Z., Smith, M., Potlurib, P., and Parnell, W. (2020), "Compression properties of polymeric syntactic foam composites under cyclic loading", Composites PartB: Engineering, 186, 107764
[2] Shearer, T., Parnell, W. J., Lynch, B., Screen, H. R. C., and David Abrahams, I. (2020) "A Recruitment Model of Tendon Viscoelasticity That Incorporates Fibril Creep and Explains Strain-Dependent Relaxation." J. Biomech. Eng. 142(7), 071003
[3] Yousaf, Z., Smith, M., Potlurib, P., and Parnell, W. (2020), "Compression properties of polymeric syntactic foam composites under cyclic loading", Composites PartB: Engineering, 186, 107764