Metamaterials and Phononic Media |

Metamaterials
Metamaterials are composite materials with bulk properties determined by their microstructure rather than their composition. They can be designed to have quite remarkable properties. This enables manipulation of waves in ways that have not been achieved with standard, or natural materials. Metamaterials are normally composed of a host material with periodic arrays of inclusions with alternative material properties. The inclusions can be solid scatterers or can be locally resonant structures themselves. The image on the right illustrates the cross-section of an array of elliptical inclusions embedded in a sidebranch resonator and was part of a collaboration with Dyson technology that led to our 2018 APL paper (see below). This microstructure was designed to half the resonance meaning that the sidebranch resonates at one-eighth of the wavelength instead of one-quarter of the wavelength. This has the potential for significant applications in space-saving attenuation mechanisms in a number of products and sectors.
It is possible to realise other specific required material parameters by adjusting the microstructure of a metamaterial, such as the period or shape of the inclusions. These features of acoustic metamaterials mean that they are of great interest in many different applications.
Metamaterials are composite materials with bulk properties determined by their microstructure rather than their composition. They can be designed to have quite remarkable properties. This enables manipulation of waves in ways that have not been achieved with standard, or natural materials. Metamaterials are normally composed of a host material with periodic arrays of inclusions with alternative material properties. The inclusions can be solid scatterers or can be locally resonant structures themselves. The image on the right illustrates the cross-section of an array of elliptical inclusions embedded in a sidebranch resonator and was part of a collaboration with Dyson technology that led to our 2018 APL paper (see below). This microstructure was designed to half the resonance meaning that the sidebranch resonates at one-eighth of the wavelength instead of one-quarter of the wavelength. This has the potential for significant applications in space-saving attenuation mechanisms in a number of products and sectors.
It is possible to realise other specific required material parameters by adjusting the microstructure of a metamaterial, such as the period or shape of the inclusions. These features of acoustic metamaterials mean that they are of great interest in many different applications.
- Parnell, W.J. and De Pascalis, R. (2019) (open access)
"Soft metamaterials with dynamic functionality tuned by pre-deformation."
Phil. Trans. A 377, 2144. (doi.org/10.1098/rsta.2018.0072) - Lynott, G, Andrew, V., Parnell, W.J., Simon, M., Abrahams, I.D. and Assier, R. (2019) (open access)
"Acoustic scattering from a two-dimensional array; tail end asymptotics for efficient evaluation of the periodic Green's function."
Wave Motion 89, 232-244. (doi.org/10.1016/j.wavemoti.2019.01.012) - Cotterill, P.A., Nigro, D., Abrahams, I.D., Garcia-Neefjes, E. and Parnell, W.J. (2018) (open access)
"Thermo-viscous damping of acoustic waves in narrow channels: a comparison of effects in air and water."
J. Acoust. Soc. America 144, 3421. (doi.org/10.1121/1.5078528) - Rowley, W.D., Parnell, W.J., Abrahams, I.D., Voisey, S.R., Lamb, J. and Etaix, N. (2018) (open access)
"Deepening subwavelength acoustic resonance via metamaterials with universal broadband elliptical microstructure"
Applied Physics Letters 112, 251902 (doi.org/10.1063/1.5022197) - Torrent, D., Parnell, W.J. and Norris, A.N. (2018) (open access)
"Loss compensation in time-dependent elastic metamaterials"
Phys. Rev. B 97, 014105 (doi.10.1103/PhysRevB.97.014105) -
Cloaking
Another application is that of "cloaking". One mechanism for this is to surround an object with a specifically designed metamaterial that can manipulate the path of propagation of incident waves to travel around the object. This means that there is no scattering by the central object, and so the object becomes acoustically invisible.
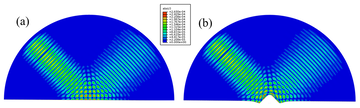
Another mechanism for cloaking is to employ materials that are deformable, or pre-stressed. The figure above, taken from our 2018 JASA paper, illustrates what happens when a so-called antiplane elastic (or "SH") wave polarise out of the plane is incident on a traction-free boundary of a half-space. One can show that if the medium is neo-Hookean and the boundary is perturbed due to an in-plane forcing, there is no change in the scattered field. This is a remarkable property of the invariant nature of neo-Hookean materials to pre-stress when subsequent SH waves pass through the medium. The medium above can therefore be thought of as a "ground cloak" in the sense that something could be placed in the gap made by the perturbation.
Another application is that of "cloaking". One mechanism for this is to surround an object with a specifically designed metamaterial that can manipulate the path of propagation of incident waves to travel around the object. This means that there is no scattering by the central object, and so the object becomes acoustically invisible.
Another mechanism for cloaking is to employ materials that are deformable, or pre-stressed. The figure above, taken from our 2018 JASA paper, illustrates what happens when a so-called antiplane elastic (or "SH") wave polarise out of the plane is incident on a traction-free boundary of a half-space. One can show that if the medium is neo-Hookean and the boundary is perturbed due to an in-plane forcing, there is no change in the scattered field. This is a remarkable property of the invariant nature of neo-Hookean materials to pre-stress when subsequent SH waves pass through the medium. The medium above can therefore be thought of as a "ground cloak" in the sense that something could be placed in the gap made by the perturbation.
- Zhang, P. and Parnell, W.J. (2018) (open access)
"Hyperelastic antiplane ground cloaking."
J Acoust. Soc. America 143 (5) (doi.org/10.1121/1.5036629) - Futhazar, G., Parnell, W.J. and Norris, A.N. (2015) (open access)
"Active cloaking for flexural waves in thin plates"
J. Sound Vibration 356, 1-19. (doi:10.1016/j.jsv.2015.06.023) - Norris, A.N., Amirkulova, F.A. and Parnell, W.J. (2014)
"Active elastodynamic cloaking"
Math. Mech. Solids 19, 603-625. (doi.org/10.1177/1081286513479962) - Parnell, W.J. and Shearer, T. (2013)
"Antiplane elastic wave cloaking using metamaterials, homogenization and nonlinear hyperelasticity"
Wave Motion 50, 1140-1152. (doi.org/10.1016/j.wavemoti.2013.06.006) - Norris, A.N., Amirkulova, F.A. and Parnell, W.J. (2012)
"Source amplitudes for active exterior cloaking"
Inverse problems 28, 105002 (doi:10.1088/0266-5611/28/10/105002) - Norris, A.N. and Parnell, W.J. (2012)
"Hyperelastic cloaking theory: Transformation elasticity with prestressed solids"
Proceedings of the Royal Society A, 468, 2881-2903. (doi:10.1098/rspa.2012.0123) - Parnell, W.J., Norris, A.N. and Shearer, T. (2012)
"Employing pre-stress to generate finite cloaks for antiplane elastic waves"
Applied Physics Letters 100, 171907, (doi:10.1063/1.4704566) - Parnell, W.J. (2012)
"Nonlinear pre-stress for cloaking from antiplane elastic waves"
Proceedings of the Royal Society A 468, 563-580, (doi:10.1098/rspa.2011.0477)
Multiple scattering in random media
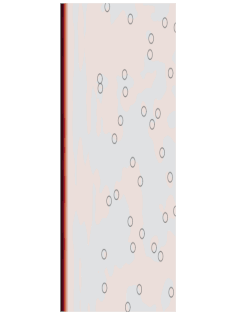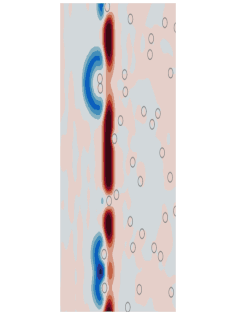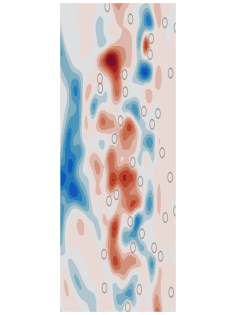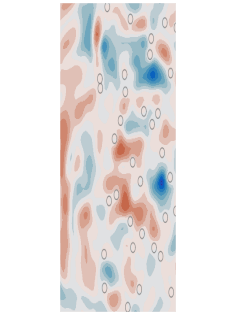
The theory of multiple scattering is employed in order to understand how a wave (of any type) scatters from multiple objects such as particles in the atmosphere, fog, objects in the ocean, inhomogeneities or defects in composites or emulsions, etc. See the animation on the right (Credit Artur Gower, University of Sheffield). The applications are broad and varied. In particular of critical importance is the ability of a theory to predict the so-called effective wavenumber of the wave when it propagates through an inhomogeneous medium. From this and/or the effective reflection and transmission coefficients the effective properties of the medium can be determined. Of course in general these are frequency dependent and also depend strongly on the volume fraction and type of scatterers comprising the medium. Since the early 1940s a mass of theory has been developed based on ensemble averaging. Our work has in the main focused on the efficacy of this theory and illustrating in particular the influence of boundaries on this effective wavenumber, or as we have shown that should be wavenumbers, i.e. more than one effective wavenumber can be shown to exist in the vicinity of the effective interface in general and in some special cases more then one wave can propagate some way into the inhomogeneous medium. The choice of such microstructures can have a profound effect on the macroscopic properties of such materials and there is a significant opportunity in order to exploit such random microstructures in metamaterial technologies.
The theory of multiple scattering is employed in order to understand how a wave (of any type) scatters from multiple objects such as particles in the atmosphere, fog, objects in the ocean, inhomogeneities or defects in composites or emulsions, etc. See the animation on the right (Credit Artur Gower, University of Sheffield). The applications are broad and varied. In particular of critical importance is the ability of a theory to predict the so-called effective wavenumber of the wave when it propagates through an inhomogeneous medium. From this and/or the effective reflection and transmission coefficients the effective properties of the medium can be determined. Of course in general these are frequency dependent and also depend strongly on the volume fraction and type of scatterers comprising the medium. Since the early 1940s a mass of theory has been developed based on ensemble averaging. Our work has in the main focused on the efficacy of this theory and illustrating in particular the influence of boundaries on this effective wavenumber, or as we have shown that should be wavenumbers, i.e. more than one effective wavenumber can be shown to exist in the vicinity of the effective interface in general and in some special cases more then one wave can propagate some way into the inhomogeneous medium. The choice of such microstructures can have a profound effect on the macroscopic properties of such materials and there is a significant opportunity in order to exploit such random microstructures in metamaterial technologies.
- Gower, A., Abrahams, I.D. and Parnell, W.J. (2019)
"A proof that multiple waves can propagate in ensemble-averaged particulate materials"
Proc. Roy. Soc. A. - Gower, A., Parnell, W.J. and Abrahams, I.D. (2019)
"Multiple waves can propagate in random particulate materials"
SIAM J. Appl. Mathematics. Accepted - Gower, A.L, Gower, R.M., Deakin, J., Parnell, W.J. and Abrahams, I.D. (2018)
"Characterising random media with near-surface backscattering: a machine learning approach for the measurement of particle size and concentration"
EuroPhysics letters 122 (5), 54001, (doi.org/10.1209/0295-5075/122/54001) - Gower, A., Smith, M.J.A., Parnell, W.J. and Abrahams, I.D. (2018) (open access)
"Reflection from a multi-species material and its transmitted effective wavenumber."
Proc. Roy. Soc. A. 474, 20170864. (doi.org/10.1098/rspa.2017.0864) - Parnell, W.J. and Abrahams, I.D. (2011)
"The effective wavenumber of a pre-stressed nonlinear microvoided composite"
Journal of Physics: Conference Series 269, 012007 (doi:10.1088/1742-6596/269/1/012007) - Parnell, W.J. and Martin, P.A. (2011)
"Multiple scattering of flexural waves by random configurations of inclusions in thin plates"
Wave Motion 48, 161-175 (doi:10.1016/j.wavemoti.2010.10.004) - Parnell, W.J. and Abrahams, I.D. (2010)
"Multiple point scattering to determine the effective wavenumber and effective properties of an inhomogeneous slab region"
Waves in Random and Complex Media 20, 678-701 (doi:10.1080/17455030.2010.510858) - Martin, P.A., Maurel, A. and Parnell, W.J. (2010)
"Estimating the dynamic effective mass density of random composites"
Journal of the Acoustical Society of America 128, 571-577 (doi:10.1121/1.3458849) - Parnell, W.J., Abrahams, I.D. and Brazier-Smith, P.R. (2010)
"Effective properties of a composite half-space: exploring the relationship between homogenization and multiple scattering theories"
Quarterly Journal of Mechanics and Applied Mathematics 63, 145-175 (doi:10.1093/qjmam/hbq002)
Phononic media
Phononic media are materials that consist of periodic arrays of inclusions or voids, the arrangement of which allows one to stop wave propagation at specific ranges of frequencies through materials via Bragg refraction and wave interference effects. Original work focused on photonics associated with light and other frequencies of electromagnetic waves. Since the 1990s however there has been a significant amount of work since there are clear applications in the area of sound, elastic waves and more recently in the area of manipulating heat flux. We have worked to develop new mathematical techniques that can help to predict the band gap structure of such periodic materials and we have also theoretically determined new material microstructures that can be deformed in order to manipulate the band gap structure. We also develop microstructures that are invariant, or almost-invariant to deformation.
Phononic media are materials that consist of periodic arrays of inclusions or voids, the arrangement of which allows one to stop wave propagation at specific ranges of frequencies through materials via Bragg refraction and wave interference effects. Original work focused on photonics associated with light and other frequencies of electromagnetic waves. Since the 1990s however there has been a significant amount of work since there are clear applications in the area of sound, elastic waves and more recently in the area of manipulating heat flux. We have worked to develop new mathematical techniques that can help to predict the band gap structure of such periodic materials and we have also theoretically determined new material microstructures that can be deformed in order to manipulate the band gap structure. We also develop microstructures that are invariant, or almost-invariant to deformation.
- Lynott, G, Andrew, V., Parnell, W.J., Simon, M., Abrahams, I.D. and Assier, R. (2019) (open access)
"Acoustic scattering from a two-dimensional array; tail end asymptotics for efficient evaluation of the periodic Green's function."
Wave Motion 89, 232-244. (doi.org/10.1016/j.wavemoti.2019.01.012) - Zhang, P. and Parnell, W.J. (2017)
"Band gap formation and tunability in stretchable serpentine interconnects."
ASME J. Applied Mechanics 84(9), 091007. (doi.10.1115/1.4037314). - Zhang, P. and Parnell, W.J. (2017) (open access)
"Soft phononic crystals with deformation-independent band gaps."
Proc. Roy. Soc. A 473, 20160865. (doi.10.1098/rspa.2016.0865) - Barnwell, E.G., Parnell, W.J. and Abrahams, I.D. (2017) (open access)
"Tunable elastodynamic band gaps"
Extreme Mechanics Letters 12, 23-29. (doi.10.1016/j.eml.2016.10.009) - Barnwell, E.G., Parnell, W.J. and Abrahams, I.D. (2016) (open access)
"Anti-plane elastic wave propagation in pre-stressed periodic structures; tuning, band gap switching and invariance"
Wave Motion 63, 98-110. (doi:10.1016/j.wavemoti.2016.02.001)
Our collaborators
|
From the UK
|
From around the world
|
