The USA reports 33 million musculoskeletal injuries per year, of which about half involve damage to soft tissues including tendons and ligaments (1). Tendon repair is often slow, and incomplete (2). An understanding of the mechanical behaviour of tendons is essential to the development of effective surgical reconstruction and prosthetic tissues.
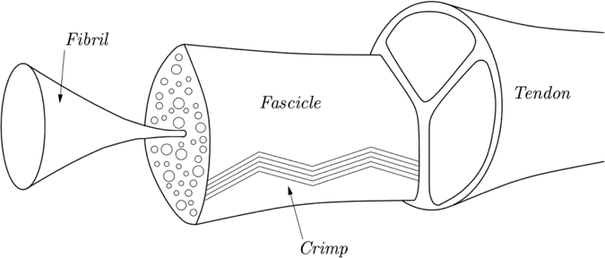
Tendons are made up of fascicles: bundles of collagen fibrils embedded in a matrix containing water, proteins such as elastin, and other substances. Fibrils are up to 60 times thinner than spider silk, and crimped (folded in a concertina fashion). Tendons connect bone to muscle, while ligaments connect bone to bone.
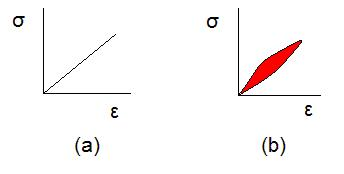
Tendons exhibit non-linear viscoelastic behaviour. Viscoelastic materials combine the behaviours of both viscous fluids and elastic solids when deformed. Their mechanical behaviour is described in terms of stress (the force applied to the material per unit area) and strain (the deformation in the material in response to stress).
In a viscoelastic material:
- A plot of stress vs strain shows hysteresis, where the state of a system depends on its history: when stress or strain is increased and then decreased, the outward and return graphs follow different curves:
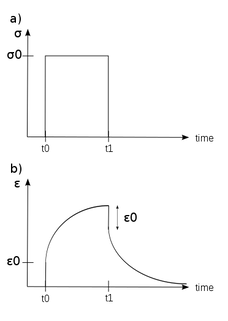
- Under a constant stress (graph a, below) the strain increases over time (the material will deform, graph b, below). This is called creep. When the stress is removed the material will slowly return to its original shape.
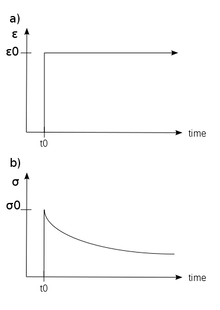
- Under a constant strain (a, below) , the stress decreases over time (stress relaxation, graph b, below)
Our model builds on existing models of tendon behaviour to account for fibril creep. We model the individual behaviour of the fibrils and matrix as linear viscoelastic, but because we allow for a distribution of different lengths of fibril in a fascicle, we can account for the non-linearity that arises in the large-scale behaviour.
Strain is a measure of the change in length of the fascicle compared to its undeformed length. We consider the fascicle to contain multiple crimped fibrils, each with a critical length, where it is fully straightened and becomes taut. The fibrils only begin to take up strain when they are taut. This is illustrated in the clip below:
When the stress is released, the fibrils begin to slacken. Because of the viscoelastic memory effect, the critical strain at which a fibril straightens will change with each sequential load.
We can illustrate the model in two tests: relaxation test and cycle test.
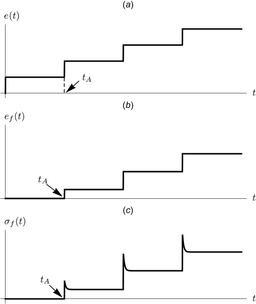
In the relaxation test the fascicle is rapidly stretched (strained), then held constant for a time, and this is repeated in a stepwise fashion, illustrated by the top graph (below, left). The middle graph shows the corresponding strain in a fibril which reaches its critical length and begins to take up strain at time tA. The bottom graph shows the fibril stress, and the relaxation effect is seen.
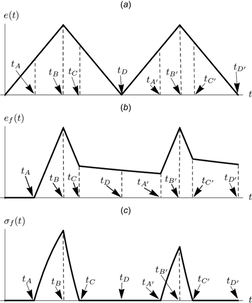
In the cycle test the fascicle is gradually stretched then unloaded. This is repeated twice (top graph, below, right). The graphs below it show the associated strain (middle) and stress (bottom) in a fibril.
On first unloading, the stress relaxation and creep effects are seen. As a result of the first cycle, the critical strain length for the second loading is longer than the first for fibrils that have taken up strain in the first cycle. For fibrils that do not straighten fully in the first cycle, the critical length will be unchanged.
The overall response of the fascicle depends on the relative proportions of matrix and fibrils, and the distribution of fibril lengths. Crucially, in our model, accounting for fibril creep allows us to predict how the fibril length distribution will evolve over time. The animations below show how the length distribution changes during the cycle test. The animation on the left does not account for fibril creep, while the one on the right does.
| | |
(1) F. Wu, M. Nerlich and D. Docheva, Tendon Injuries, Basic Science and New Repair Proposals, EFORT Open Reviews, 2017, 2, 332-342 10.1302/2058-5241.2.160075
(2) R. James, G. Kesturu, G. Balian and A. Chhabra, Tendon: Biology, Biomechanics, Repair, Growth Factors, and Evolving Treatment Options, The Journal of Hand Surgery, 2008, 33, 102-112 doi.org/10.1016/j.jhsa.2007.09.007
 RSS Feed
RSS Feed