$$ \begin{equation} g(t)=A \cos(2\pi f t) \label{eq:eq1} \end{equation}$$
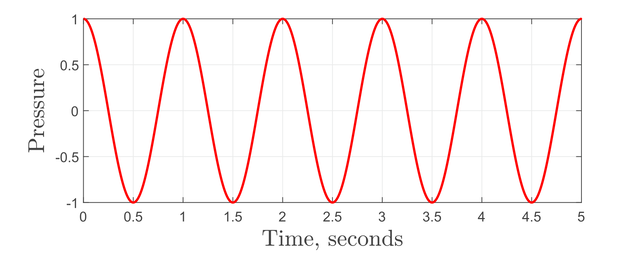
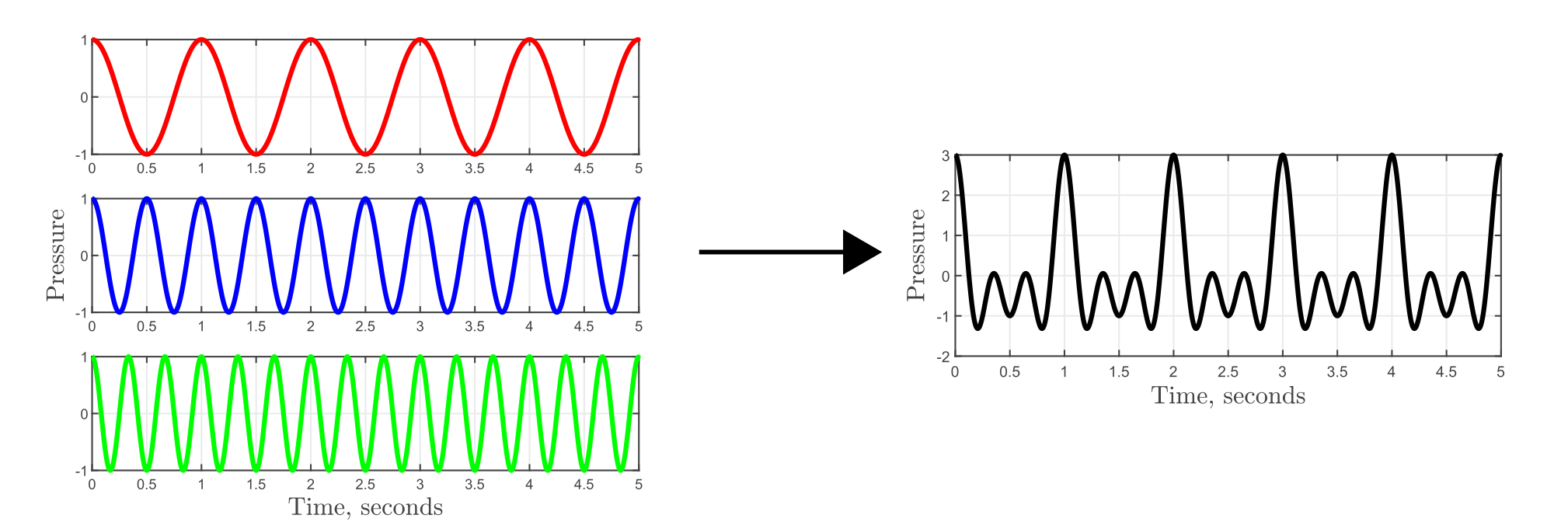
When the peaks of the waves meet, the pressure field is amplified, and where the the peaks meet the troughs the pressure cancels out. We call this process of overlapping waves to create a non wave-like pressure field superposition. Sound recorded by a microphone is much more likely resemble the pressure field on the right hand side of Figure 2, than the wave in Figure 1. However, for us to look at the complex pressure field it it difficult to identify its component frequencies. In fact, not only can certain sound fields be created by the superposition of waves, but any sound field can be produced by a unique combination of waves.
$$\begin{equation} G(f)=\int_\infty^\infty g(t) \exp\{2\pi i f t\}\, dt, \label{eq:eq2}\end{equation}$$
where \(\exp\{-\}\) is the exponential operator, and \( i = \sqrt{-1}\).
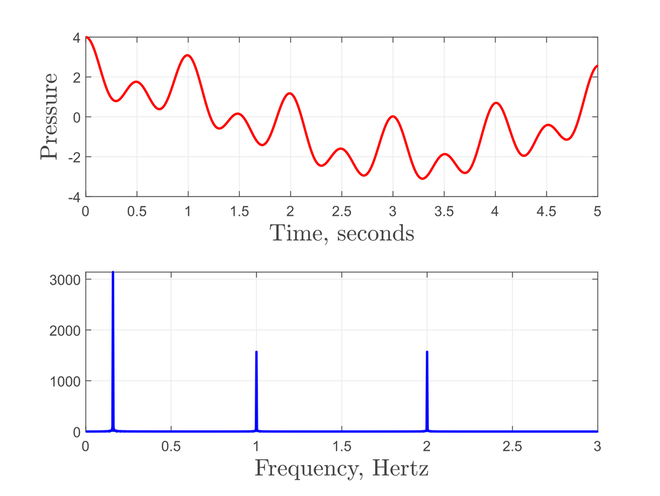
In Figure 3 the first graph shows the resulting field of three waves in superposition, with frequencies \(f = 1/2\pi\), \(f = 1\) and \(f = 2\), given by
$$\begin{equation} g(t)=2\cos(t)+\cos(2\pi t)+\cos(4 \pi t). \label{eq:eq3}\end{equation}$$
The Fourier transform is not limited to use in sound processing and analysis: it can be applied to any system where there is known to be an oscillating energy source which can operate at a continuous spectrum of frequencies. For example, the Fourier transform is used in a wide range of spectroscopy techniques such as Nuclear Magnetic Resonance (NMR) spectroscopy which uses the Fourier transform to analyse the magnetic fields of atomic nuclei.
 RSS Feed
RSS Feed