Noise pollution can reduce our quality of life, and even our life expectancy. A 2014 report from the European Environment Agency estimates that 10,000 premature deaths and 43,000 hospital admissions for coronary heart disease and stroke can be attributed to noise exposure in Europe each year. (1) The urgent need for efficient noise cancellation devices is clear.
Destructive Interference
Here’s how it works:
The animation below shows how a QWR functions:
There are limitations to this approach: the size of the resonator depends on the wavelength of the noise we want to reduce. Low frequency noises have long wavelengths, so the size of the resonator required soon becomes impractically large.
Acoustic Metamaterials
Metamaterials are special materials with properties that are not found in conventional materials. Unlike conventional materials, the properties of metamaterials are defined by their structures rather than by their chemical make-up. Acoustic metamaterials have geometries that allow the manipulation of sound waves in ways not previously achievable.
Our metamaterial has arrays of elliptical cylinders which stretch the apparent space inside the resonator, with the result that the effective speed of sound is reduced by half. Crucially, it does this while maintaining a close match to the impedance of sound in air across a range of frequencies.
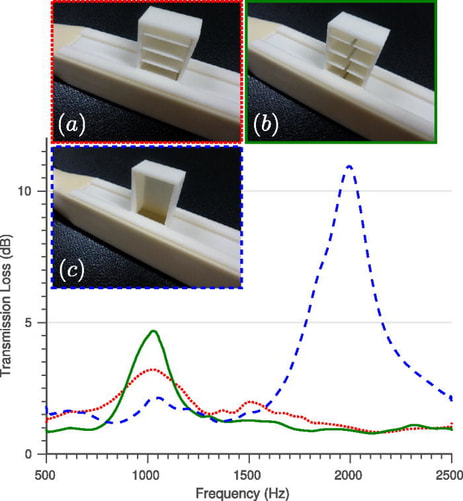
Space-Saving Devices
When the speed of sound is halved, either the length of the resonator, or the frequency of the sound it reduces must also be halved. This allows significant space savings and opens up the possibility of building more practical, size efficient devices for the reduction of low frequency noise.
Read the full paper here: doi.org/10.1063/1.5022197
(1) European Environment Agency Report No. 10/2014: www.eea.europa.eu/publications/noise-in-europe-2014









 RSS Feed
RSS Feed