
The daughter of a bourgeois Parisian silk merchant, Sophie’s early interest in mathematics grew during the reign of terror, which kept her confined to the family home. Sophie found intellectual stimulation in her father’s library, and spent long hours studying mathematics, Greek and Latin; teaching herself the latter in order to understand texts by Newton and Euler. This interest in intellectual pursuits was initially strongly disapproved of by her parents, who removed her candles and her fire in a vain attempt to discourage her studies. They eventually relented, however, realising that their daughter was serious in her work.
Image source: http://mathshistory.st-andrews.ac.uk/PictDisplay/Germain.html
As a young woman, Sophie was barred by her sex from attending the newly established Ecole Polytechnique, but was able to obtain the lecture notes and submit work under the borrowed name of Monsieur Leblanc, a former student who had left the city. She was to use this same pseudonym in her initial correspondence with mathematicians including Legendre, Lagrange and Gauss, fearing that as a woman, she would not be taken seriously. On discovering Germain’s true identity, however, Gauss responded with admiration for her tenacity.
Germain was particularly interested in number theory, but a visit to Paris by Ernst Chladni in 1808 turned her attention in another direction. Chladni reproduced his classic experiment, producing nodal figures in sand on vibrating plates. In response, in 1809 the Institut de France offered a kilo of gold to any person who could formulate a mathematical theory of elastic surfaces.
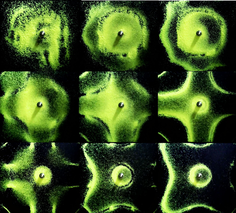
It is likely that, being self taught, and lacking in formal education and guidance, there were gaps in Germain’s knowledge that affected her work in mathematical physics more than her work in number theory. However, this makes her achievements in the field all the more extraordinary. Germain took a different approach to that of her rival in the early days of the challenge, Siméon-Denis Poisson, whose initial work on the problem was based on molecular theory. Poisson was admitted to the institute early in the competition (something not permitted to Germain) and became a judge rather than a competitor. As such, he had access to Germain’s work, and she consulted with him on the subject. However Poisson did not regard Germain as a serious scholar, and did not acknowledge her in his own 1814 work on elasticity.
In later life, Germain continued her work in both number theory and elasticity. She contributed to the body of work on Fermat’s Last Theorem with what became known as “Sophie Germain’s Theorem”, published in a supplement to the second edition of Legendre’s Théorie des Nombres. Before her death from breast cancer in 1831, Germain published her work on surface curvature, Mémoire sur la courbure des surfaces. After the intervention of Gauss, Sophie Germain was eventually awarded a posthumous honorary degree from the University of Göttingen.
References and further reading
- Del Centina, A., Fiocca, A., (2012), ‘The correspondence between Sophie Germain and Carl Friedrich Gauss’, Arch. Hist. Exact Sci. 66:585–700
- Laubenbacher, R., Pengelley, D., (2010), ‘Voici ce que j’ai trouvé: Sophie Germain’s grand plan to prove Fermat’s Last Theorem’, Historia Mathematica 37 (2010) 641–692
- Frize, M. (2010). The Bold and the Brave: A History of Women in Science and Engineering. Ottawa: University of Ottawa Press.
- GRAY, M. (2005). Sophie Germain. In CASE B. & LEGGETT A. (Eds.), Complexities: Women in Mathematics (pp. 68-74). Princeton; Oxford: Princeton University Press.
- Bucciarelli L.L., Dworsky N. (1980) An Award with Reservations. In: Sophie Germain. Studies in the History of Modern Science, vol 6. Springer, Dordrecht.
- https://scientificwomen.net/women/germain-sophie-39
- http://mathshistory.st-andrews.ac.uk/Biographies/Germain.html
- https://simonsingh.net/books/fermats-last-theorem/sophie-germain/
- https://www.thoughtco.com/sophie-germain-biography-3530360
 RSS Feed
RSS Feed