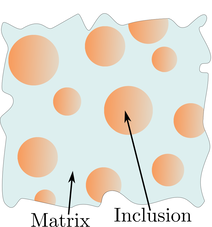
| Inclusions of all different shapes and sizes can be used to intentionally alter the effective properties of a composite material. For example, reinforcing brittle concrete with steel rods to increase its strength or, on a smaller scale, embedding highly conductive fibres throughout a less conductive matrix to improve heat dissipation. In both cases, the material properties of the matrix and inclusions complement each other and result in a more practical composite material. On the other hand, sometimes engineers are forced to incorporate inclusions into their designs; adding windows along the side of commercial aircraft for instance. In this case, the material properties can be affected in undesirable (and occasionally catastrophic) ways. |
| A famous example is the world's first jetliner, the Comet, in 1952. The pressurised cabins were designed with large, squared-off windows causing pressure to repeatedly build-up at the corners. At high altitudes the corners of a window could be subjected to pressure up to three times higher than the rest of the cabin. Unfortunately, in several cases, this resulted in fatal structural damage. To avoid this problem, aircraft are now designed with the rounded, porthole-style windows we see today, however, neutral inclusions could offer an alternative approach. |
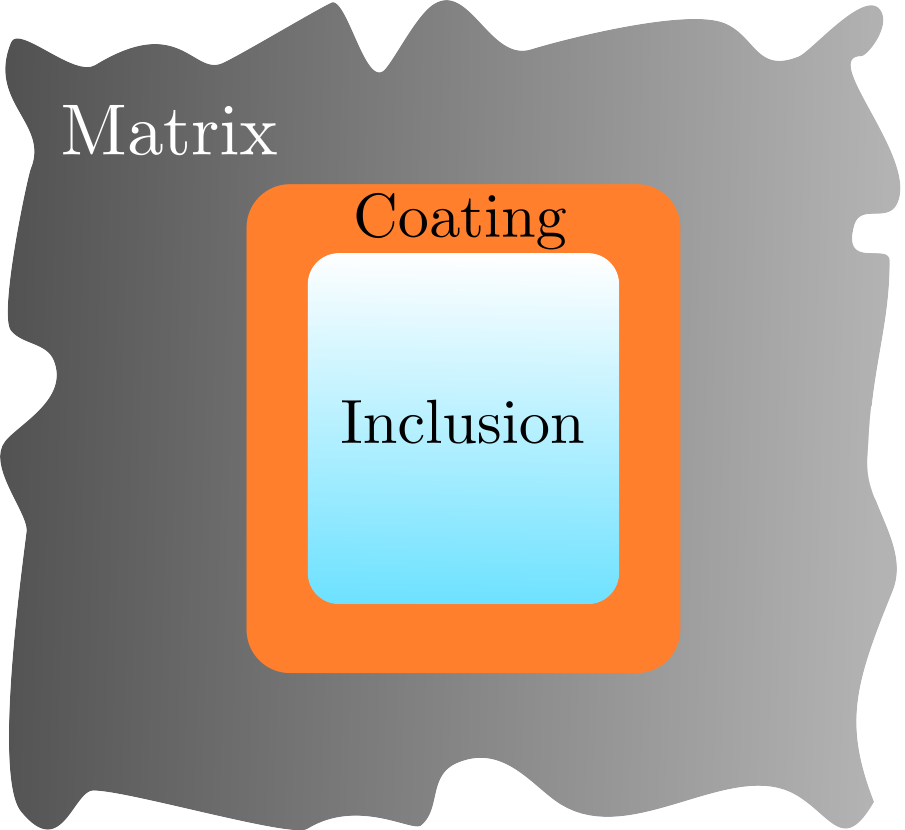
| For example, we could surround the squared-off windows of the Comet with an additional coating to relieve the pressure from its corners. The required properties of the coating will depend on both the matrix (the cabin wall) and the inclusion (the window). If the necessary properties are satisfied the combination of the inclusion and its coating is referred to as a neutral inclusion and the fields in the matrix become unperturbed. All we need now is to determine the required properties within the coating. To show how we approach this problem we consider perturbations within the temperature field of a matrix. |
We are interested in the temperature field, \(T(\mathbf{x})\), which must satisfy the heat equation. For this example, we assume the thermal conductivity is isotropic (independent of direction) and homogeneous (independent of position) and is therefore a scalar. As a result, together with the steady-state assumption, the heat equation reduces to Laplace's equation, given by:
$$\begin{equation}
\nabla ^2 T(\mathbf{x}) = 0,
\label{laplace}
\end{equation}$$
where \(\nabla ^2\) is the Laplace operator.
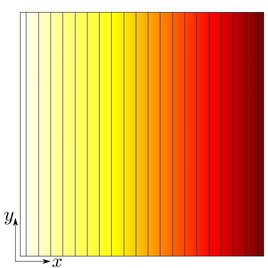
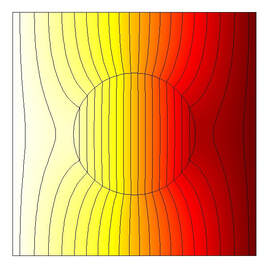
Let the matrix in Figure 1 have conductivity \(k_m\). Notice in Figure 2 that when a circular inclusion with conductivity \(k_i\), where \(k_i \neq k_m\), is embedded in the matrix, the field becomes perturbed and is no longer linear.
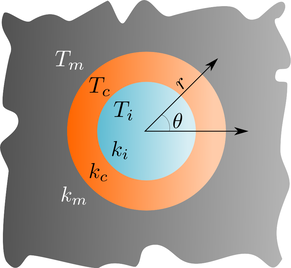
| The temperature fields in the matrix, coating and inclusion are denoted by \(T_m(\mathbf{x}),\ T_c(\mathbf{x})\) and \(T_i(\mathbf{x})\) respectively and must all satisfy Laplace's equation. We solve (1) for all temperature fields to find: $$ \begin{equation} \begin{split} &T_m(r,\theta) = \left(\alpha r + \dfrac{B_m}{r}\right) \sin \theta, \\ &T_c(r,\theta) = \left(A_c r + \dfrac{B_c}{r}\right) \sin \theta, \\ &T_i(r,\theta) = A_i r \sin \theta, \label{temp fields} \end{split} \end{equation} $$ where \(B_m,\ A_c,\ B_c\) and \(A_i\) are constants. |
Let the radius of the inclusion and coating be given by \(r_i\) and \(r_c\) respectively. Solving the temperature fields in (2) with perfect contact conditions across each interface (continuity of heat flux and temperature) we find that \(B_m=0\) is satisfied when
\begin{equation}
D^2 = \dfrac{(k_m-k_c)(k_i+k_c)}{(k_i-k_c)(k_m+k_c)} \qquad \text{where} \qquad D= \dfrac{r_i}{r_c}
\label{k cond}
\end{equation}
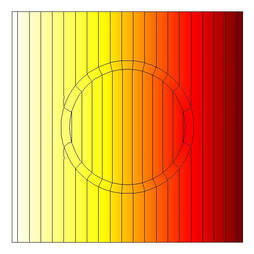 Figure 4: Neutral Inclusion leading to unperturbed field in the matrix
Figure 4: Neutral Inclusion leading to unperturbed field in the matrix 2.2 Neutral inclusions: extensions and limitations
As we are not restricted to a single coating, we can extend the work in the previous section with as many additional coatings as we wish. For example, a bi-layer neutral inclusion where an inner coating insulates its core region, protecting the inclusion from external forces, and an outer coating counteracts any perturbations caused by the insulator. Since the inclusion may have any material properties, the bi-layer neutral inclusion acts as a cloak for the specific problem it is designed for.
A perfect cloak is one which, regardless of the external forces, leads to unperturbed fields in the matrix. Transformation theory is used to design perfect cloaks and other interesting concepts. We will discuss these in a future blog post.

 RSS Feed
RSS Feed