In 1995 a group of Spanish physicists demonstrated that a kinetic artwork by artist Eusebio Sempere, consisting of a periodic arrangement of steel rods, selectively attenuated sound at a frequency of 1670 Hz. Sempere's sculpture, similar in concept to the one pictured below, is an example of a phononic crystal [1].
Phononic crystals (PCs) interact with sound and elastic waves in ways not found in conventional materials. Like Sempere's sculptures, they have periodic structures and typically contain regular arrangements of one material held in a host or matrix material.
Both phononic crystals and acoustic metamaterials allow the manipulation of sound waves, but while metamaterials rely on micro-structures that are very much smaller than the wavelengths in question, phononic crystals typically have repeating units on a larger scale.
One of the remarkable and useful properties of phononic crystals is the frequency band gap. This is a range of frequencies of acoustic or elastic waves that cannot propagate through the material. The PC acts as a selective filter, eliminating specific frequencies of unwanted vibration or noise.
The image below illustrates this phenomenon. Along the x-axis we plot the wave vector, which describes the physical property of the wave and specifically the direction in which it propagates. The y-axis corresponds to the frequency. The area shaded in green highlights a gap in the frequencies through which no wave vector passes, meaning that no waves in this frequency range can propagate in the material.
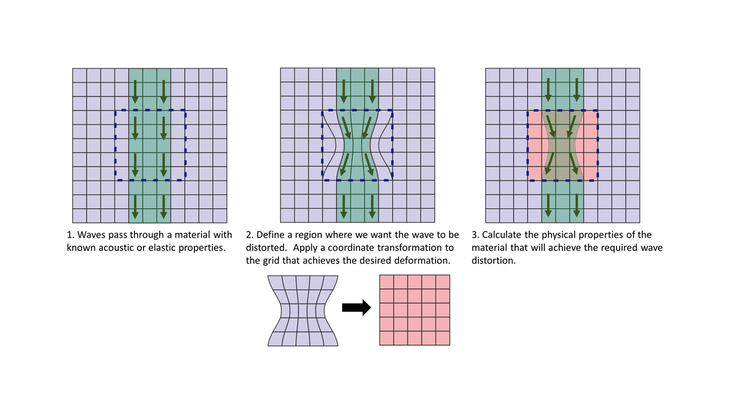
Phononic crystals and acoustic metamaterials can be designed through a process called transformation acoustics (where sound waves are concerned), or transformation elasticity (the equivalent for elastic waves).
This stepwise process is summarised in the image below. The desired wave manipulation is first defined in terms of a spatial, or coordinate transformation. Then the physical properties of a material capable of achieving this wave distortion are calculated.
The Lagrangian elasticity tensor quantifies the elasticity of a material in the Lagrangian specification: a frame of reference in which a medium (e.g. a fluid) is observed from the point of view of its material particles. The Lagrangian point of view is sometimes described as analogous to observing the flow of a river from a boat floating on the water. The alternative, Eulerian specification would be like observing from a fixed position on the riverbank [4].
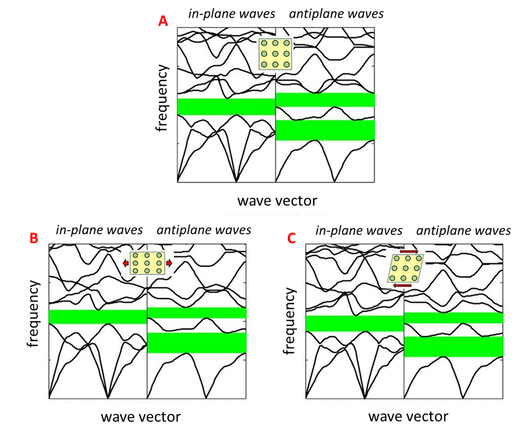
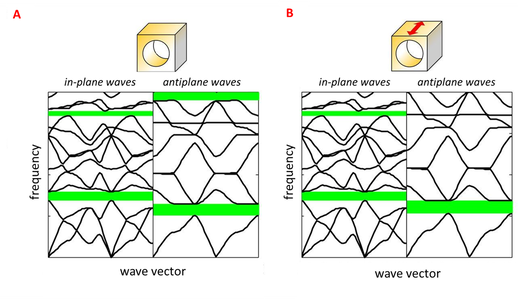
We derived the properties of soft PCs that fulfil this requirement. Two examples are described here. Both require a hyperelastic, or rubber-like matrix phase. The first model contains an arrangement of stiff aluminium cylinders, and the second contains a regular distribution of cylindrical voids.
The figure below shows the band structure for in-plane and out-of plane waves in the first model. A is the undeformed case, B shows the case where the material is stretched in the direction of the red arrows, and C depicts a shear deformation. The shear deformation has negligible effect on band gaps for waves in either direction, and the effect of the stretch deformation is only slight.
- R. Martinez-Sala, J. Sancho J. V. Sanchez, V. Gomez J. Llinares and F. Meseguer, Sound attenuation by sculpture, Nature, 1995, 378(16), 241
- E.G. Barnwell, W. J. Parnell, and I. D. Abrahams, Anti-plane elastic wave propagation in pre-stressed periodic structures; tuning, band gap switching and invariance, Wave Motion, 2016, 63, 98-110. doi.org/10.1016/j.wavemoti.2016.02.001
- K. Bertoldi and M. C. Boyce, Mechanically triggered transformations of phononic band gaps in periodic elastomeric structures, Phys. Rev. B, 2008, 77, 052105. https://journals.aps.org/prb/abstract/10.1103/PhysRevB.77.052105
- Lagrangian vs Eulerian frame of reference:https://www.youtube.com/watch?v=iDIzLkic1pY



 RSS Feed
RSS Feed