When we wanted to make a short video about the design of metamaterials for noise reduction devices, we turned to illustrator and comedian John Cooper.
John has worked on projects for the University of Manchester before, creating work for the University’s School Governor Initiative and for the Children’s University of Manchester. His humorous style lends clarity and informality to a topic.
We started from a blog post about the piece of research in question. John used it to sketch out an initial storyboard proposal featuring noisy geese! We then put together an initial script, from which John created a slideshow storyboard.
Here’s what John had to say, ‘I really enjoyed this project. The work the department does is fascinating, and it was an exciting challenge in generating visuals to complement their work on noise reduction. It's good to learn new things while being creative.’
Here’s the finished product. Watch out for those geese!





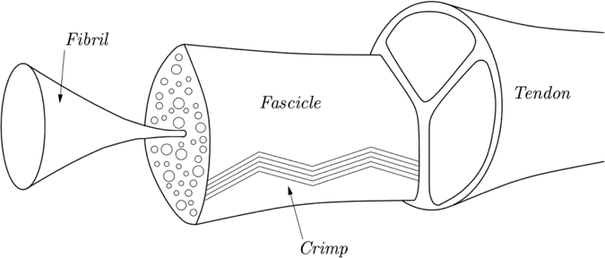
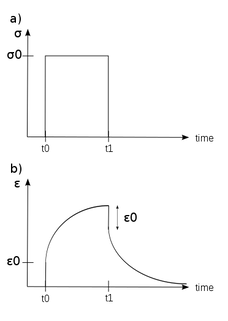
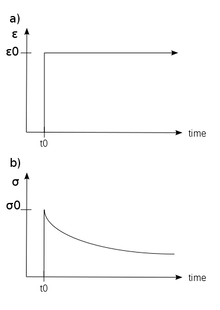
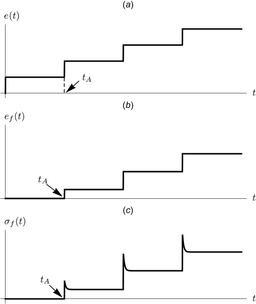








 RSS Feed
RSS Feed